13 Linear Predictors and Inverse Link Functions
The above mosaic is put here to emphasize that we are learning building blocks for making models of data-generating processes. Each block is used to make some mathematical representation of the real-world. The better our representations, the better our insights. Instead of using Lego bricks, our tool of choice is the generative DAG. We have almost all the building blocks we need, latent nodes, observed nodes, calculated nodes, edges, plates, linear models, and probability distributions, but this chapter introduces one last powerful building block - the inverse link function.
The range of a function is the set of values that the function can give as output. For a linear predictor with non-zero slope, this range is any number from -\(\infty\) to \(\infty\).
13.1 Linear Predictors
This chapter, we focus on restricting the range of linear predictors. A linear predictor for data observation, \(i\), is any function expressable in this form:
\[ f(x_{i1},x_{i2},\ldots,x_{in}) = \alpha + \beta_1 * x_{i1} + \beta_2 * x_{i2} + \cdots + \beta_n * x_{in} \]
where \(x_{i1},x_{i2},\ldots,x_{in}\) is the \(i^{th}\) observation of a set of \(n\) explanatory variables, \(\alpha\) is the base-level output when all the explanatory variables are zero (e.g. y-intercept when \(n=1\)), and \(\beta_j\) the coefficient for the \(j^{th}\) explanatory variable (\(j \in \{1,2,\ldots,n\}\)). When \(n=1\), this is just the equation of a line as in last chapter. When there is more than one explanatory variable, we are making a function with high-dimensional input - meaning the input includes multiple explanatory RV realizations per observed row. High-dimensional functions are no longer easily plotted, but the interpretation of the coefficients remain consistent with our developing intuition.
Explanatory variable effects are fully summarized in the corresponding coefficients, \(\beta\). If an individual coefficient \(\beta\) is positive, the linear prediction increases by \(\beta\) units for each unit change in the explanatory variable. For example, we thought it plausible for the expected sales price of a home to go up by $120 for every additional square foot; 10 additional square feet, then the home value increases $1,200; 100 additional square feet, then the home value increases $12,000. You can continue this logic ad-nauseum until you have infinitely big houses with infinite home prices. The takeaway is that linear predictors, in theory, can take on values anywhere from -\(\infty\) to \(\infty\).
13.2 Inverse Link Functions
An inverse link function takes linear predictor output, which ranges from -\(\infty\) to \(\infty\), and confines it in some way to a different scale. For example, if we want to use many explanatory variables to explain success probability, our method will be to estimate a linear predictor and then, transform it so its value is forced to lie between zero and 1 (i.e. match the domain over which probabilities exist). More generally, inverse link functions are used to make linear predictors map to predicted values that are on a different scale. For our purposes, we will look at two specific inverse link functions:
- Exponential: The exponential function converts a linear predictor of the form \(\alpha + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n\) into a curve that is restricted to values between 0 and \(+\infty\). This is useful for converting a linear predictor into a non-negative value. For example, the rate of tickets issued in New York city can be modelled by taking a linear predictor for tickets and turning it into a non-negative rate of ticket issuance. If we label the linear predictor value \(y\) and the transformed value \(\lambda\), the exponential function converting \(y\) to \(\lambda\) is defined here: \[ \lambda = \exp(y) = \alpha + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n \]
- Inverse Logit (aka logistic): This function provides a way to convert a linear predictor of the form \(\alpha + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n\)) into a curve that is restricted to values between 0 and 1. This is useful for converting a linear predictor to a probability. If we label the linear predictor value \(y\) and the transformed value \(\theta\), the inverse logit function converting \(y\) to \(\theta\) is defined here (note the negative sign): \[ \theta = \frac{1}{1+\exp(-y)}= \frac{1}{1+\exp(-(\alpha + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n))} \]
While the beauty of these functions is that it allows us to use the easily-understood linear model form and still also have a form that is useful in a generative DAG. The downside is we lose interpretability of the coefficients. The only thing we get to say easily is that higher values of the linear predictor correspond to higher values of the transformed output.
When communicating the effects of explanatory variables that are put through inverse link functions, you should either: 1) simulate observed data using the prior or posterior’s generative recipe, or 2) consult one of the more rigorous texts on Bayesian data analysis for some mathematical tricks to interpreting generative recipes with these inverse link functions (see references at end of book).
13.2.1 Exponential Function
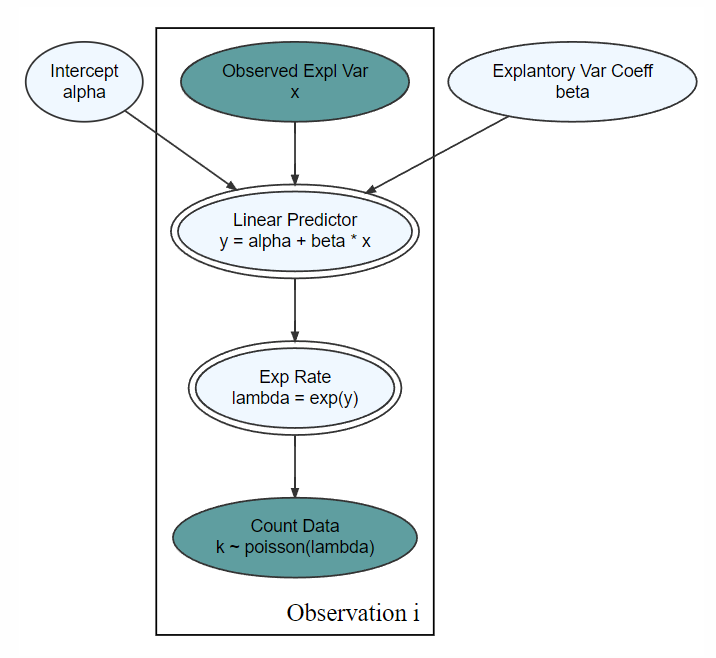
Figure 13.1 takes a generic example of a Poisson count variable and makes the expected rate of occurrence a function of an explanatory variable.
For a specific example, think about modelling daily traffic ticket in New York City. The expected rate of issuance would be a linear predictor based on explanatory variables such as inches of snow, holiday, president in town, end-of-month, etc. Since linear predictors can turn negative and the rate parameter of a Poisson random variable must be strictly positive, we use the exponential function to get from linear predictor to rate.
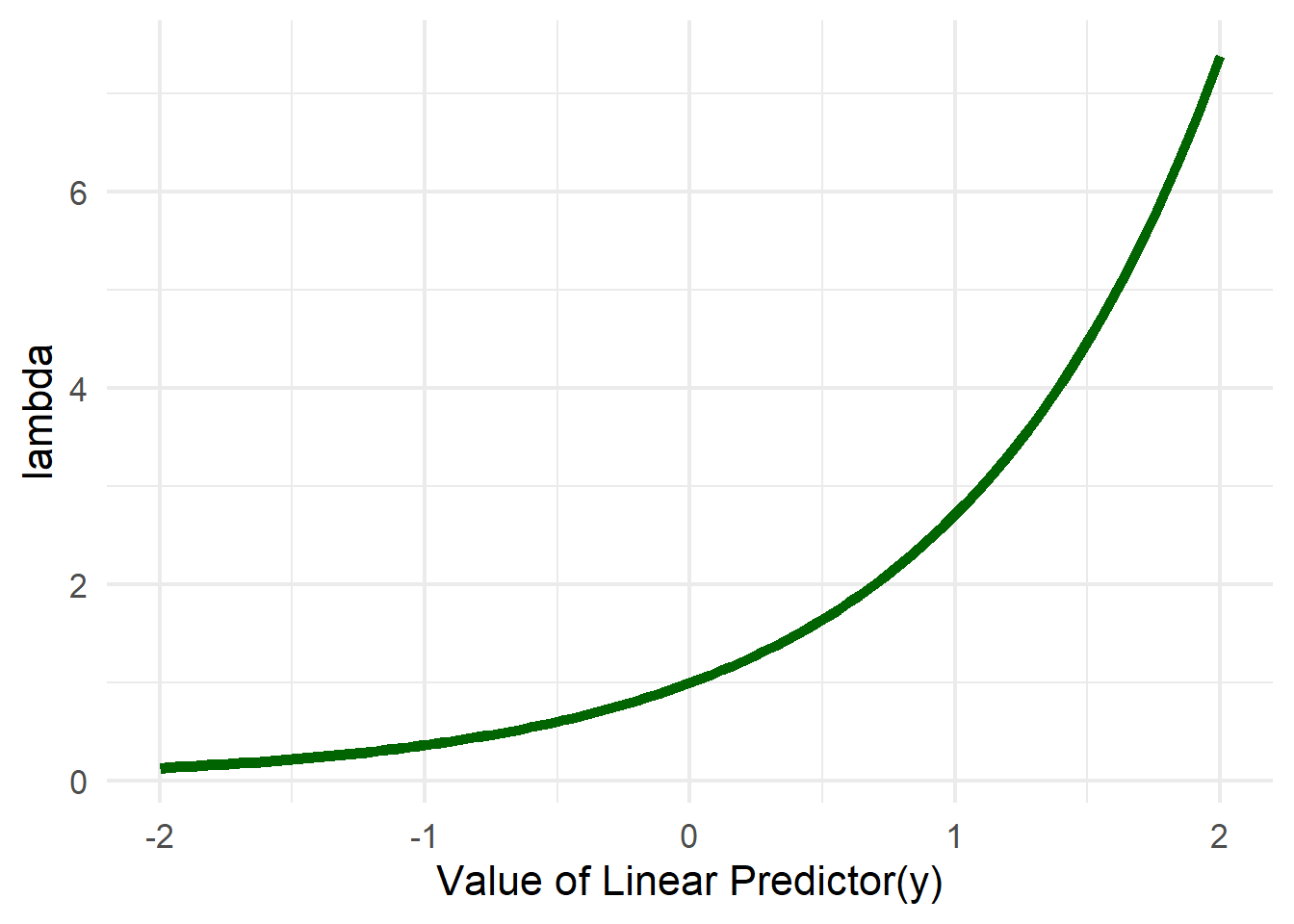
The inverse link function transformation takes place in the node for lambda. The linear predictor, \(y\), can take on any value from -\(\infty\) to \(\infty\), but as soon as it is transformed, it is forced to being a positive number. This transformation is shown in Figure Figure 13.2.
From Figure 13.2, we see that negative values of \(y\) are transformed into values of \(\lambda\) between 0 and 1. As \(y\) goes positive and increases, \(\lambda\) values also get higher, but in a non-linear manner.
13.2.2 Inverse Logit
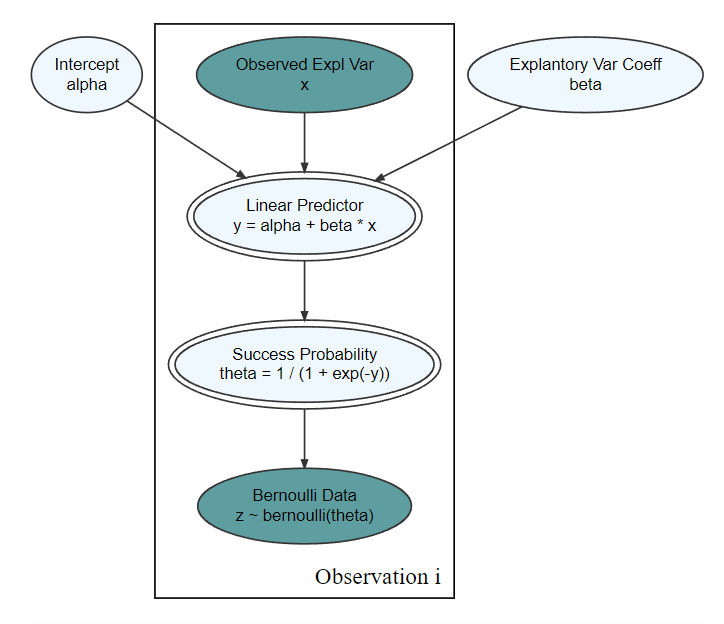
Figure 13.3 shows a generic generative DAG which leverages the inverse logit link function.
The use of the inverse logit function is done inside a method called logistic regression. Check out this sequence of videos that begin here https://youtu.be/zAULhNrnuL4 on logistic regression for some additional insight.
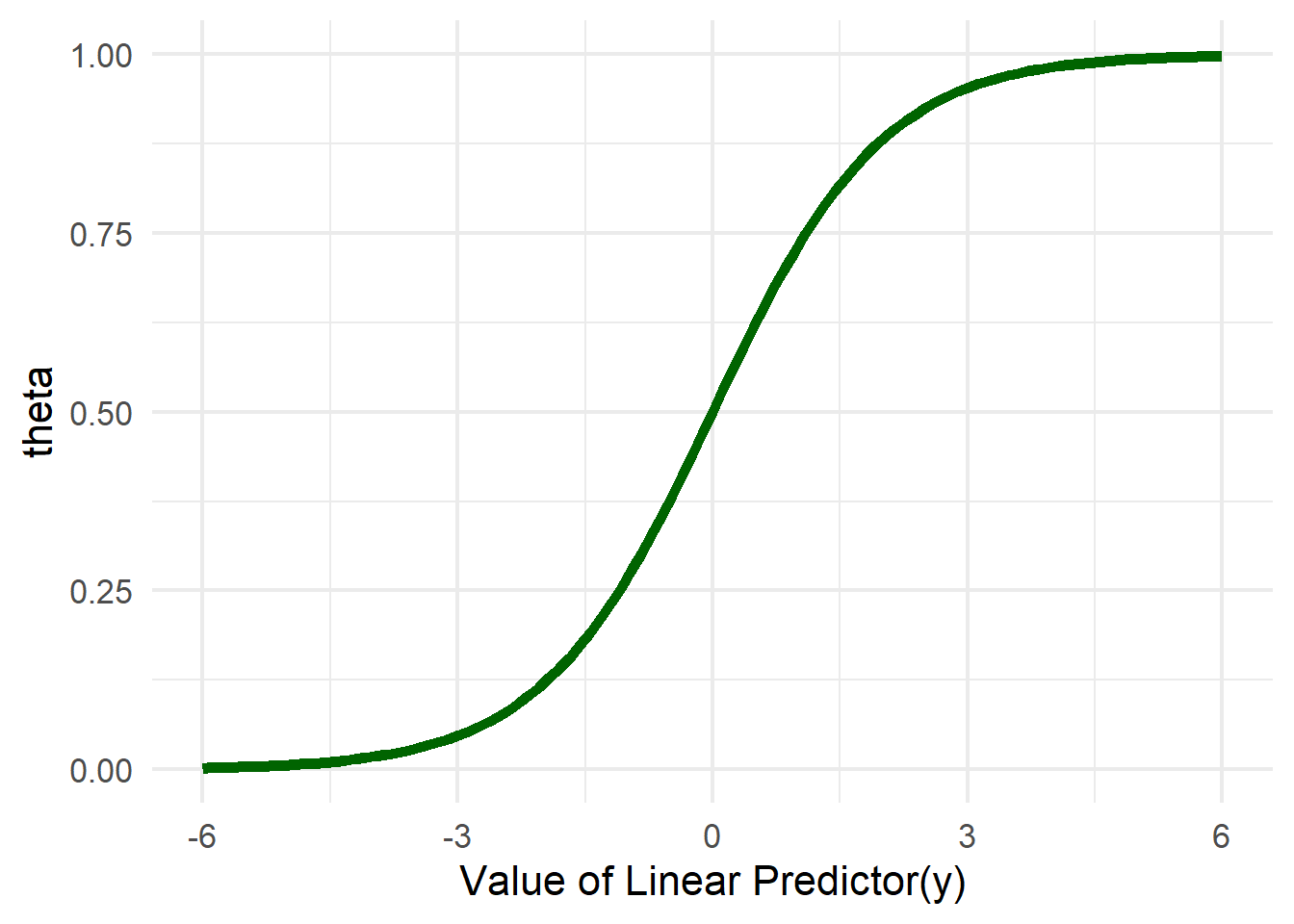
Note the inverse link function transformation takes place in the node for theta. To start to get a feel for what this transformation does, observe Figure 13.4. When the linear predictor is zero, the associated probability is 50%. Increasing the linear predictor will increase the associated probability, but with diminishing effect. When the linear predictor is increased by one unit from say 1 to 2, the corresponding probability goes from about 73% to 88% (i.e. from \(\frac{1}{1+\exp(-1)}\) to \(\frac{1}{1+\exp(-2)}\)). This is a 15% jump. However, increasing the linear predictor by one additional unit has probability go from 88% to 95% - only a 7% jump. Further increasing the linear predictor has diminishing effect. Likewise, large negative values in the linear predictor lead to ever-closer to zero values for probability.
13.3 Building Block Training Complete
You have officially been exposed to all the building blocks you need for executing Bayesian inference of ever-increasing complexity. These include latent nodes, observed nodes, calculated nodes, edges, plates, probability distributions, linear predictors, and inverse-link functions. While you have not seen every probability distribution or every inverse-link, you have now seen enough that you should be able to digest new instances of these things. In the next chapter, we seek to build confidence by increasing the complexity of the business narrative and the resulting generative DAG to yield insights. Insights you might not even have thought possible!
13.4 Getting Help
TBD
13.5 Questions to Learn From
See CANVAS.